이 글은...
Andrew Ng 교수의 Deep Learning 강좌 C1W3L07까지의 내용을 정리한 것이다. 활성화 함수의 종류와 비선형 함수를 사용해야 하는 이유에 대해 알아보았다.
내용 요약
활성화 함수
활성화 함수는 여러 종류가 있을 수 있다. 지금까지는 시그모이드 함수만 다루었는데, 이를 대체할 수 있는 대표적인 활성화 함수를 알아보았다.
- Tanh
- $a={{e^{z}-e^{-z}}\over{e^{z}+e^{-z}}}$
- 형태가 시그모이드와 유사하게 생겼다.
- 원점을 지나고 기울기가 다르다.
- 출력값 범위가 -1과 1 사이이다.
- 평균이 0이기 때문에 데이터가 원점을 중심으로 이동하게 된다.

- ReLU (Rectified Linear Unit)
- $a=max(0,z)$
- 활성화 함수 입력값이 0보다 클 때 미분 값이 시그모이드나 Tanh보다 더 잘 학습할 수 있다.
- 대부분의 학습에 적합하다.
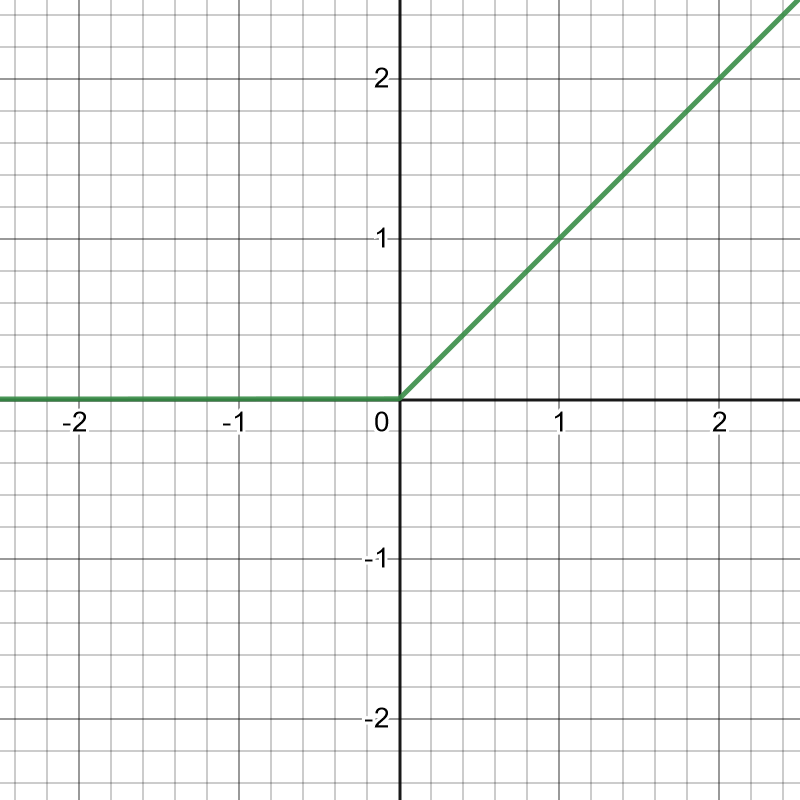
중요한 것은 이진 분류로 결과가 나와야 하는 학습 모델에서는 출력 층에 반드시 시그모이드를 사용해야 한다. 왜냐하면 0과 1 사이의 값으로 결과가 나와야 하기 때문이다. 은닉층은 뭘 사용하든 상관없다.
왜 비선형 활성화 함수를 써야할까
선형 함수란 아래와 같은 함수를 말한다.
$y=x$
$y=ax$
$y=ax+b$
이런 형태의 활성화 함수를 사용한다 했을 때, 여러 개의 은닉층이 쌓여도 아무런 이득이 없다. 여기서 이득이 없다고 하는 것은 은닉층이 많이 쌓이더라도 1층짜리와 별다를 게 없다는 것을 의미한다. 예를 들어 $g(z)=z$라는 활성화 함수를 사용했을 때 3개 층이 쌓여도 $g(g(g(z)))=z$이기 때문이다.
'연구 노트 > 머신러닝' 카테고리의 다른 글
| [TIL] 210414 - Deep LearniNg (~C1W4L11) (0) | 2021.04.14 |
|---|---|
| [TIL] 210413 - Deep LearniNg (~C1W3L09) (0) | 2021.04.13 |
| [TIL] 210406 - Deep LearniNg (~C1W3L05) (0) | 2021.04.06 |
| [TIL] 210405 - Deep LearniNg (~C1W3L03) (0) | 2021.04.05 |
| [TIL] 210401 - Deep LearniNg (~C1W2L18) (0) | 2021.04.02 |


