이 글은...
Andrew Ng 교수의 Deep Learning 강좌 C1W2L07 까지의 내용을 정리한 것이다. 비용함수의 결과값을 최저로 만드는 파라미터를 어떻게 찾아야 하는지 설명한다. 그리고 그 과정에 필요한 미분의 개념을 간단히 살핀다.
내용 요약
경사 하강법
비용함수의 값을 최소화하는 $w$와 $b$를 찾는데 사용할 수 있는 방법이다. 이때 비용함수는 볼록한(convex) 형태여야 한다. 만약 비용함수의 형태가 볼록하지 않다면 지역 최솟값을 여러 개 가지게 되어 진짜 최솟값을 찾기 어려워진다.
비용함수의 최솟값을 찾기 위한 시작점은 임의로 정하여도 상관없다. 경사 하강법을 사용하면 어디에서 시작하든 최솟값이 있는 곳으로 향하게 된다. 가파른 방향으로 한 스텝씩 업데이트하며 최솟값을 찾아간다.
$w:=w-\alpha{\partial{J(w,b)}\over\partial{d}}$
$b:=b-\alpha{\partial{J(w,b)}\over\partial{d}}$
미분
딥러닝을 익히는 데에는 미분에 대한 직관만 가지고 있어도 충분하다고 한다. 미분이란 함수의 기울기이며 어떤 한 지점의 변화량을 말한다.
$f(a)=3a\rightarrow {df(a) \over da}=3$
$f(a)=a^2\rightarrow {df(a) \over da}=2a$
$f(a)=\log_{e} a=\ln a\rightarrow {df(a) \over da}={1 \over a}$
계산 그래프
정방향 전파, 역방향 전파를 이해하는데 기반이 되는 개념이다. 3개의 인자를 갖는 함수를 계산하는 과정을 예시로 들었다.
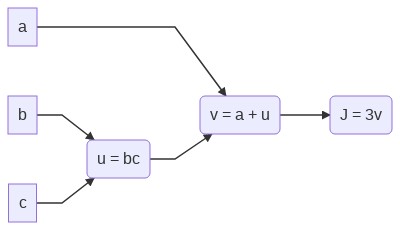
$J(a,b,c)=3(a+bc)$라는 함수가 있을 때 아래처럼 계산 과정을 나눌 수 있다.
$u=bc$
$v=a+u$
$J=3v$
그리고 이것을 그래프로 그리면 아래와 같다.
'연구 노트 > 머신러닝' 카테고리의 다른 글
| [TIL] 210331 - Deep LearniNg (~C1W2L15) (0) | 2021.03.31 |
|---|---|
| [TIL] 210330 - Deep LearniNg (~C1W2L13) (0) | 2021.03.30 |
| [TIL] 210329 - Deep LearniNg (~C1W2C10) (0) | 2021.03.29 |
| [TIL] 210325 - Deep LearniNg (~C1W2L03) (0) | 2021.03.25 |
| [TIL] 210324 - Deep LearniNg (~C1W1L04) (0) | 2021.03.24 |


